In computer science , an AVL tree (named after inventors A delson-V elsky and L andis) is a self-balancing binary search tree . It was the first such data structure to be invented.[2] In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O (log n ) time in both the average and worst cases, where $n$ is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations .
Wikipedia
需要解决的问题 二叉搜索树(Binary Search Tree)上的基本操作所花费的时间与树高成正比。对于“常规”的二叉搜索树来说,插入及查找所需的时间复杂度都为$O(logN)$,但是如果对一个有序序列构建二叉搜索树,就会造成树一边偏的情况——这时树退化为偏树(Skewed Tree)或链表,最坏时间复杂度上升到$O(N)$,成为一种设计极不合理的数据结构。
与快速排序一样的思路,要解决这个问题,我们需要随机打乱构建树的序列,让它不再那么“有序”。
但是生活就像一盒巧克力,你永远不知道下一颗是什么味道,在大多数情况下我们不能预先知道构建序列是怎么样的。
定义 我们定义一个平衡因子 BF(Balance Factor)来表示树上每一个结点当前的平衡状态:
那么,AVL 树是如何保持 BF 一直满足定义的呢?
平衡的保持 从一个单独的结点开始算,此时树中只有一个根节点,根节点的 BF 为 0,显然该树是一棵 AVL 树。
随着结点的每次插入,递归更新所有受影响结点的 BF,直到出现插入后打破规则的结点——找到离插入结点 INSERT_NODE 最近的、 BF 绝对值大于 1 的结点 SUB_ROOT ,以 SUB_ROOT 为根结点对该子树(称为最小不平衡子树 )进行调整使其满足平衡的标准。
综上可将调整的规律分为 4 种旋转类型:
LL-rotation 左孩子的左子树
RR-rotation 右孩子的右子树
LR-rotation 左孩子的右子树
RL-rotation 右孩子的左子树
下面分别介绍插入结点在不同位置时对应的旋转策略,其中 A 结点为 SUB_ROOT ,红色为需要嫁接的子树。
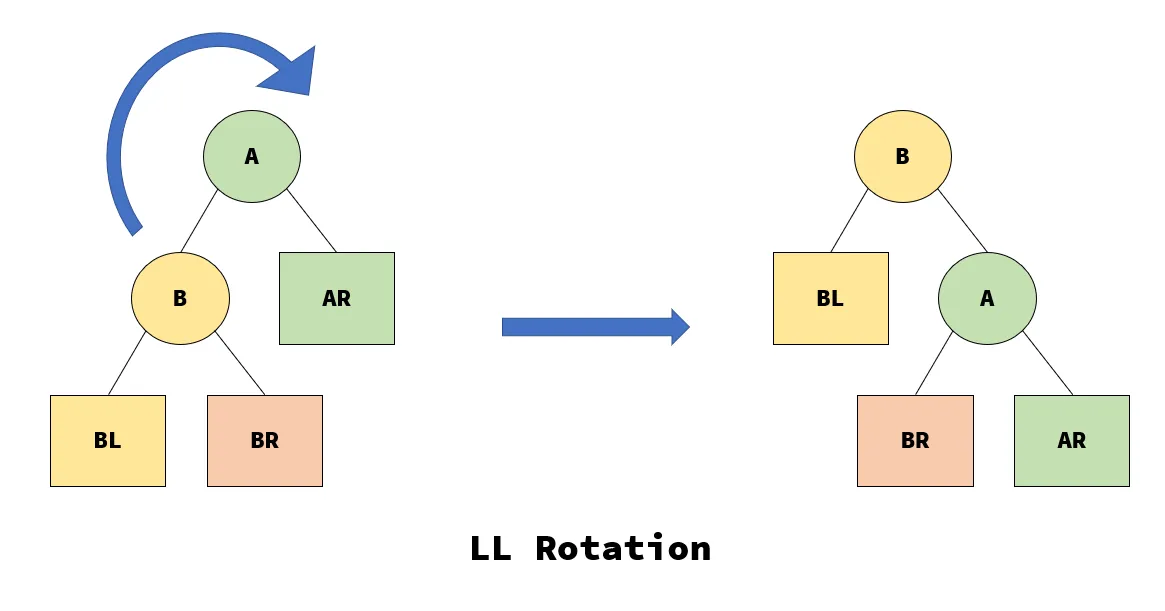
LL Rotation
如图,由于结点 A 的左孩子的左子树插入结点导致的不平衡,使用LL旋转进行调整。将 A 的左孩子 B 向上旋转成为根结点,相应地 A 向下旋转成为 B 的右孩子,并将 B 的原右子树 BR 接到 A 的左孩子处。
这样旋转过后,B 和 BL 的高度减少了 1,其余部分高度增加 1,使得左右子树恢复平衡。
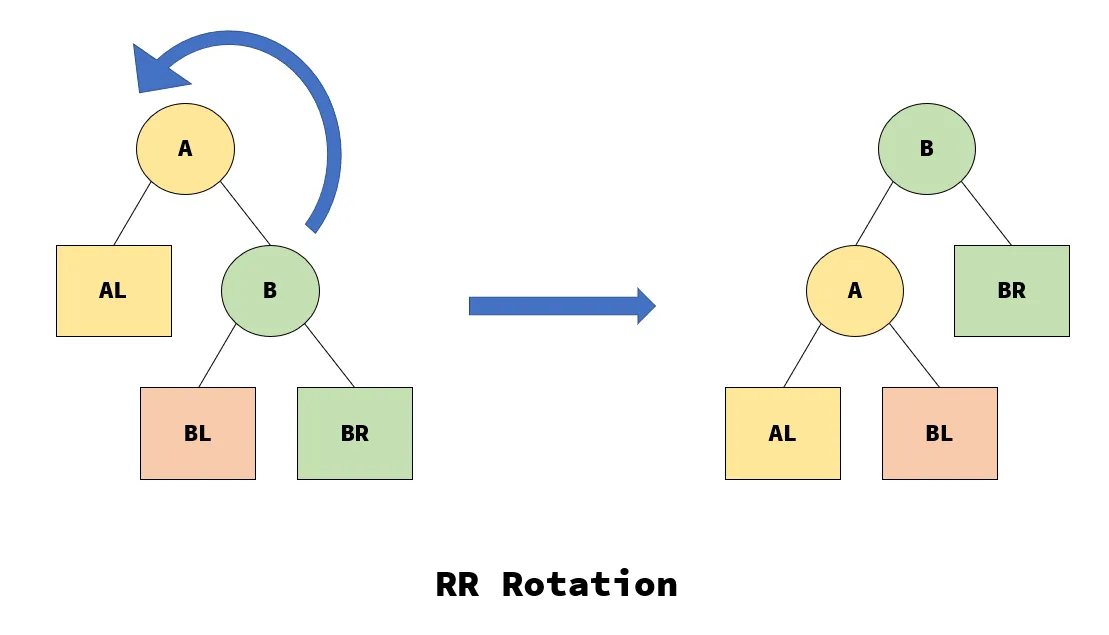
RR Rotation
同理,经过一次旋转之后,整个子树恢复平衡。
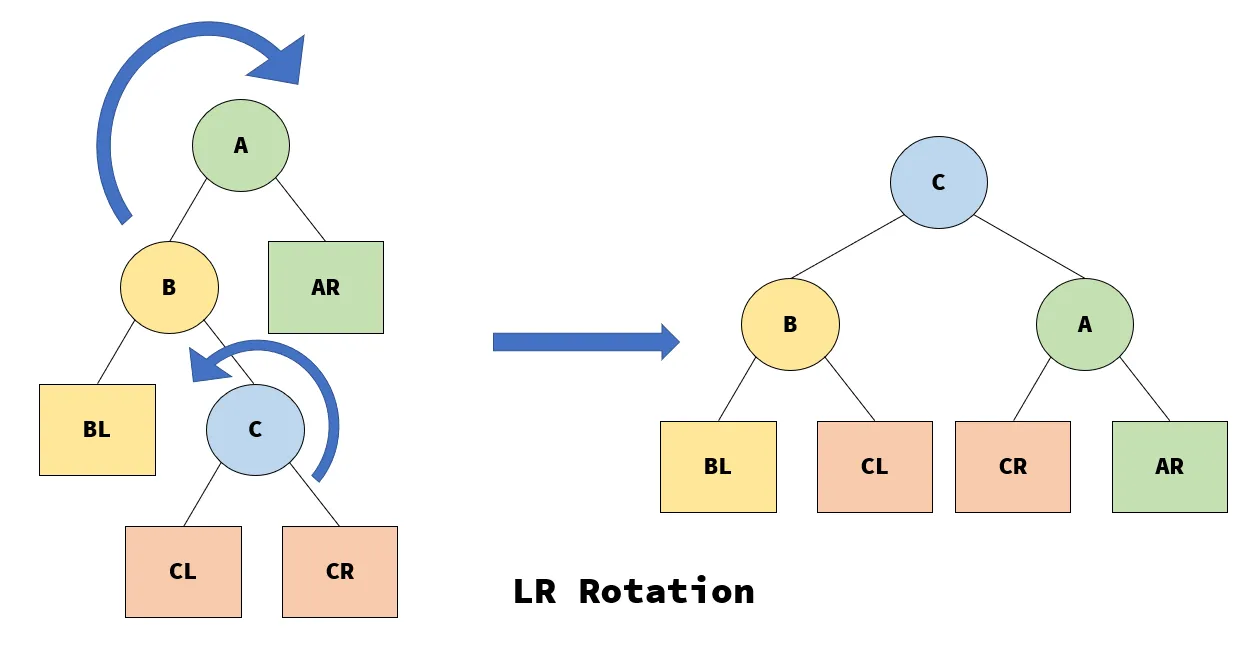
LR Rotation
如果新插入的结点在 A 的左孩子的右子树上,那么对应的旋转策略也会复杂一些。
这里使用两次旋转即可解决,首先对以 B 为根结点的子树进行 RR 旋转,再对以 A 为结点的子树进行 LL 旋转即可。
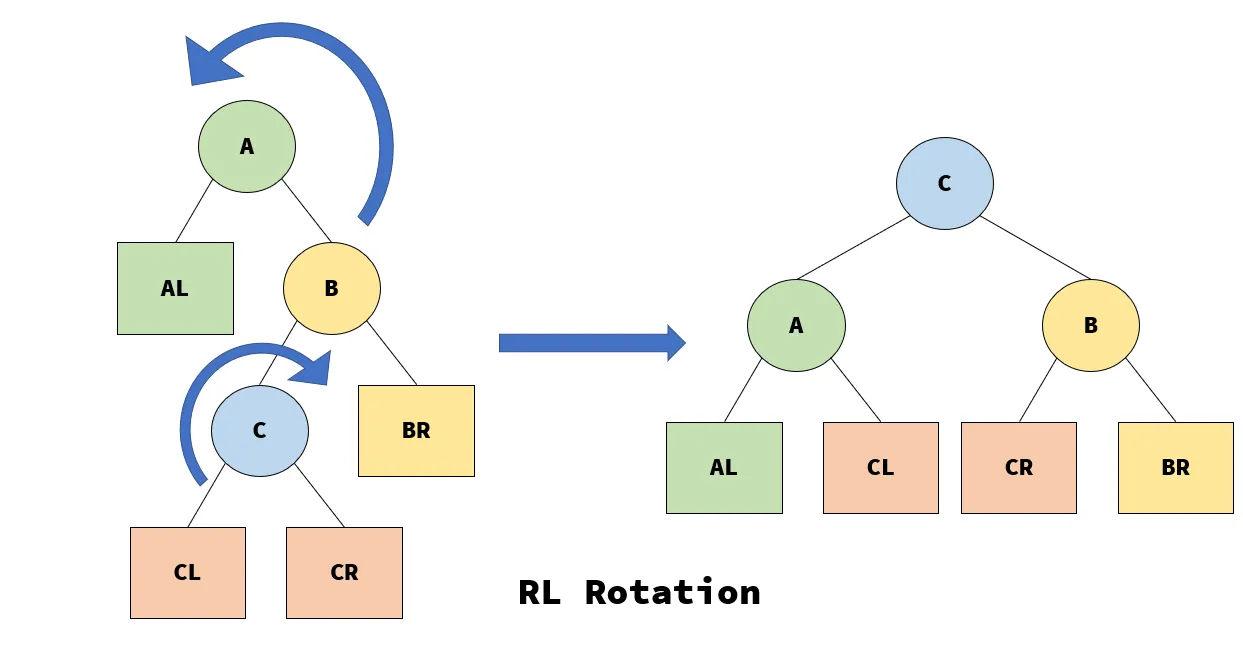
RL Rotation
同理,首先对以 B 为根结点的子树进行 LL 旋转,再对以 A 为结点的子树进行 RR 旋转即可。
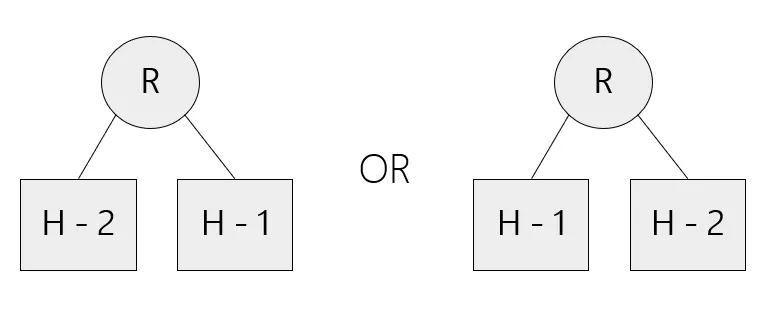
复杂度 由 AVL 树的定义可知,一棵树高为 $H$ 的 AVL 树一定满足以下形式之一:
其中 R 指根节点,它的子树高度一定为 $H - 1$ 或 $H - 2$,因此我们令 $N_H$ 为树高为 $H$ 的 AVL 树的最少结点数,得到递推式:
$$
$$
$$
两边取对数:
C++ 实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 #include <iostream> #include <bits/stdc++.h> using namespace std;template <typename T>class AVL_tree {private : struct node { T val; node *left, *right; int height; node (T v) : val (v), left (nullptr ), right (nullptr ) {} }; node *ROOT = nullptr ; int _height(node *cur) { return cur ? cur->height : 0 ; } bool _balance(node *cur) { const int balance_factor = _height(cur->left) - _height(cur->right); return balance_factor <= 1 && balance_factor >= -1 ; } void _re_height(node *cur) { cur->height = max (_height(cur->left), _height(cur->right)) + 1 ; } node *LL_rotation (node *cur) { node *ptr = cur->left; cur->left = ptr->right; ptr->right = cur; _re_height(cur); _re_height(ptr); return ptr; } node *RR_rotation (node *cur) { node *ptr = cur->right; cur->right = ptr->left; ptr->left = cur; _re_height(cur); _re_height(ptr); return ptr; } node *LR_rotation (node *cur) { cur->left = RR_rotation (cur->left); return LL_rotation (cur); } node *RL_rotation (node *cur) { cur->right = LL_rotation (cur->right); return RR_rotation (cur); } node *_insert(node *cur, T &x) { if (!cur) { cur = new node (x); } else { if (x >= cur->val) { cur->right = _insert(cur->right, x); if (!_balance(cur)) { if (cur->right->val > x) { cur = RL_rotation (cur); } else { cur = RR_rotation (cur); } } } else { cur->left = _insert(cur->left, x); if (!_balance(cur)) { if (cur->left->val <= x) { cur = LR_rotation (cur); } else { cur = LL_rotation (cur); } } } } _re_height(cur); return cur; } bool _contains(node *cur, T &x) { if (!cur) { return false ; } if (cur->val > x) { return _contains(cur->left, x); } if (cur->val < x) { return _contains(cur->right, x); } return true ; } public : AVL_tree () = default ; void insert (T x) ROOT = _insert(ROOT, x); } bool contains (T x) return _contains(ROOT, x); } vector<T> level_order () { vector<T> rt; if (!ROOT) { return rt; } deque<node *> dq; dq.emplace_back (ROOT); while (!dq.empty ()) { node *ptr = dq.front (); if (ptr->left) { dq.emplace_back (ptr->left); } if (ptr->right) { dq.emplace_back (ptr->right); } rt.emplace_back (ptr->val); dq.pop_front (); } return rt; } }; int main () vector<int > seq = {5 , 7 , 90 , 12 , 1 , 50 }; AVL_tree<int > Tree; for (auto &it : seq) { Tree.insert (it); } for (auto it : Tree.level_order ()) { cout << it << " " ; } }